“熵”的介绍
信息熵(Information entropy)是信息论中的概念,由香农( mathematician Claude Shannon)在其论文“A Mathematical Theory of Communication”提出的。它衡量事件所包含的信息量。一般而言,事件的不确定性或者随机性越大,则它包含的信息越多。
例如,如果一个人被告知他已知道的信息,则他获取的信息是很少的。告知某人已知道的信息,是没有意义的,则说这些信息具有较低的熵;反之,如果一个人被告知他不知道的信息,则他获取的信息是很多的。这些信息对他而言是有价值的,表明这些信息具有加高的熵。
“熵”的定义
这里讨论离散的情况。对于离散随机变量 $X=\lbrace x_1,x_2,\cdots,x_n \rbrace$,其概率分布为$P(X)=\lbrace p(x_1),p(x_2),\cdots,p(x_n) \rbrace$,则该离散随机变量 $X$ 的熵定义为: \begin{equation} H(X)=E[-\ln(P(X))]=-\sum_{i=1}^{n}{p(x_i)\log_{b}{p(x_i)}} \end{equation} 熵的本质是香农信息量($\log(P(X))$)的期望。
“交叉熵”
关于样本集的2个概率分布 $P$ 和 $Q$,其中 $P$ 为真实分布, $Q$ 为估计(预测)分布。按照真实的分布 $P$ 来衡量识别一个样本的所需要的编码长度的期望(平均编码长度)为: \begin{equation} H(p)=-\sum_{i}{p(x_i)\log_{b}{p(x_i)}} \end{equation} 如果用估计的分布 $Q$ 来表示真实分布 $P$ 的平均编码长度,则为: \begin{equation} H(p,q)=-\sum_{i}{p(x_i)\log_{b}{q(x_i)}} \end{equation} 将 $H(p,q)$ 称之为“交叉熵”。
举例说明
例一
考虑抛均匀的硬币这一个案例。 抛掷均匀硬币,此时下一次抛掷结果的不确定的熵是最大的。因为出现正反面是等概率的,均为0.5,不确定性最大,其结果也最难预测。其熵计算如下: \begin{equation*} H(X)=-\sum_{i=1}^{n}{p(x_i)\log_{b}{p(x_i)}}=-\sum_{i=1}^{2}{\frac{1}{2} \log_{2}(\frac{1}{2})}=1 \end{equation*}
如果硬币不均匀,即出现正反面的概率不等,则下一次抛掷结果的不确定性减少了,因为因为有更大的可能性出现某一面。如假设出现正面的概率为$p=0.7$,则反面出现的概率为$q=0.3$。此时,熵的计算如下: \begin{equation*} H(X)=-p\log_2(p)-q\log_2(q)=-0.7\log_2(0.7)-0.3\log_2(0.3) \approx 0.881 < 1 \end{equation*}
最极端的例子是硬币两面一样,则不管如何抛掷硬币结果都一样,没有提供新的信息,不存在不确定性,此时的熵则为0。
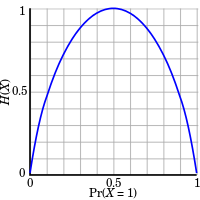
下图展示了抛掷硬币出现某一面的概率大小对熵的变化大小。
例二
猜测球的颜色游戏:人甲拿出一个球,人乙猜球的颜色,猜对游戏停止,否则继续猜测。当答案只剩下两种选择时,猜测游戏结束,无论猜对猜错都能$100\%$的确定答案,无需再猜一次。
题目一: 有橙、紫、蓝及青四种颜色的小球任意个,各颜色小球的占比不清楚,现在从中拿出一个小球,猜所拿出的小球是什么颜色?
在这种情况下,各色小球数量未知,只能认为四种颜色的小球出现的概率是一样的。所以,根据下图策略 $1$,各小球颜色只需要猜两次。
 故,期望的猜球次数为:\(H=\frac{1}{4}*2 + \frac{1}{4}*2 + \frac{1}{4}*2 + \frac{1}{4}*2=2\)
故,期望的猜球次数为:\(H=\frac{1}{4}*2 + \frac{1}{4}*2 + \frac{1}{4}*2 + \frac{1}{4}*2=2\)
题目二: 箱子里面有小球任意个,知道其中 $\frac{1}{2}$ 是橙色球,$\frac{1}{4}$ 是紫色球,$\frac{1}{8}$ 是蓝色球及 $\frac{1}{8}$ 是青色球。现在从中拿出一个小球,猜所拿出的小球是什么颜色?
很明显,在这种情况下,橙色占比二分之一,如果猜测橙色,很有可能第一次就猜中。故根据下图策略,$\frac{1}{2}$ 的概率是橙色求,只需要猜测一次;$\frac{1}{4}$ 的概率是紫色求,只需要猜测两次;$\frac{1}{3}$ 的概率是蓝色求,只需要猜测三次;$\frac{1}{8}$ 的概率是青色求,只需要猜测三次;

故,期望的猜球次数为:\(H=\frac{1}{2}*1 + \frac{1}{4}*2 + \frac{1}{8}*3 + \frac{1}{8}*3=1.75\)
题目三: 箱子里面有小球任意个,知道全部是橙色球。现在从中拿出一个小球,猜所拿出的小球是什么颜色?
很明显,拿出的球肯定是橙色,需要猜测 $0$ 次。
总结–信息熵
上面三个题目表现出这样一种现象:针对特定概率为 $p$ 的小球,需要猜球的次数为 $\log_2{(1/p)}$,例如题目二中,$1/4$ 是紫色球,需猜测 $\log_2{4}=2$ 次,$1/8$ 是蓝球,需猜测 $\log_2{8}=3$ 次。那么,针对这个过程,预期的猜题次数为: \begin{equation} \sum_{k=1}^{N}{p_k \log_{2}{\frac{1}{p_k}}} \end{equation}
这就是信息熵。信息熵代表的是随机变量或整个系统的不确定性,熵越大,随机变量或系统的不确定性就越。第一题的信息熵为 $2$,第二题的信息熵为 $1.75$,最三题的信息熵为 $0$,题目一的熵 > 题目二的熵 > 题目三的熵。题目一,由于对整个系统一无所知,只能假设所有的情况出现的概率都是均等的,此时的熵是最大的;题目二中,知道了各颜色小球出现的概率,说明小明对这个系统有一定的了解,所以系统的不确定性自然会降低,所以熵小于 $2$;题目三中,已经知道箱子中全部都是橙色球,拿出的球肯定是橙色的,因而不确定性为0,也就是熵为0。所以,在什么都不知道的情况下,熵会最大,针对上面的题目一 ~ 题目三,这个最大值是 $2$,除此之外,其余的任何一种情况,熵都会比 $2$小。
上述题目中,已知的概率分布,称之为真实分布,如题目一中的 $\lbrace \frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4} \rbrace$ 和题目二中的 $\lbrace \frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{8} \rbrace$。根据真实分布,能够找到一个最优策略,以最小的代价消除系统的不确定性,而这个代价大小就是信息熵。信息熵衡量了系统的不确定性,而我们要消除这个不确定性,所要付出的【最小努力】(猜题次数、编码长度等)的大小就是信息熵。具体来讲,题目1只需要猜两次就能确定任何一个小球的颜色,题目2只需要猜测1.75次就能确定任何一个小球的颜色。
总结–交叉熵
回到题目二,已知小球的真实分布是 $\lbrace \frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{8} \rbrace$,然而,猜球者忽略了小球的真实分布,任然固执的认为所有小球出现的概率相同,为 $\lbrace \frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4} \rbrace$,这个分布就是非真实分布,或者预计/估计的分布。
此时,猜测的期望次数是:\(H=\frac{1}{2}*\log_2{4} + \frac{1}{4}*\log_2{4} + \frac{1}{8}*\log_2{4} + \frac{1}{8}*\log_2{4}=2\)。
很明显,针对题目二,使用题目一中的策略是一个坏的选择,因为需要猜题的次数增加了,从$1.75$变成了$2$。因此,当根据系统的真实分布制定最优策略去消除系统的不确定性时,所付出的努力是最小的;当然,也许会使用其他的策略(非真实分布)去消除系统的不确定性,则所付出的努力是有所增加。那么,当我们使用非最优策略消除系统的不确定性,所需要付出的努力的大小我们该如何去衡量呢?使用交叉熵。
交叉熵,其用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。其定义见交叉熵定义。将题目一中策略用于题目二,真实分布为 $P=\lbrace \frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{8} \rbrace$,非真实分布为 $Q=\lbrace \frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4} \rbrace$,则交叉熵为\(\frac{1}{2}*\log_2{4} + \frac{1}{4}*\log_2{4} + \frac{1}{8}*\log_2{4} + \frac{1}{8}*\log_2{4}=2\),比最优策略的 $1.75$ 大。
因此,交叉熵越低,这个策略就越好,说明这个策略越接近最优策略。最低的交叉熵也就是使用了真实分布所计算出来的信息熵。因此,当 $P=Q$ 时,交叉熵=信息熵。因此,在机器学习分类算法中,常用交叉熵作为代价函数,寻求最小交叉熵,因为交叉熵越低,就证明由算法所产生的策略最接近最优策略,也间接证明我们算法所算出的非真实分布(根据样本计算的分布)越接近真实分布。
