看到深度学习如此火爆,神经网络相关资料层出不穷,不禁想起研究生阶段上过的神经网络课程,似懂非懂。这次兴起,仔细看了下应用最广泛的神经网络之一的 BP 神经网络,介绍如下文所示。
简介
BP (back propagation) 神经网络是1986年由 Rumelhart 和 McClelland 为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络。
基本原理
BP 神经网络是一种按误差反向传播训练的多层前馈网络,其算法称为 BP 算法。利用梯度下降法,调整神经网络中的权重参数,以期使网络的实际输出值和期望输出值的误差均方差为最小,即使得预测输出跟踪给定输出。
计算过程
BP 神经网络的计算包括两个过程:正向计算和反向计算。
- 正向计算:输入层数据经隐含层逐层处理,最终转向输出层,得出实际输出;
- 反向计算:将实际输出与期望输出间的误差信号沿着网络连接通路反向传播,辅助修正各神经元的权重,以期误差信号最小。
现在以一个典型的三层神经网络为例说明参数的计算推理调整过程。
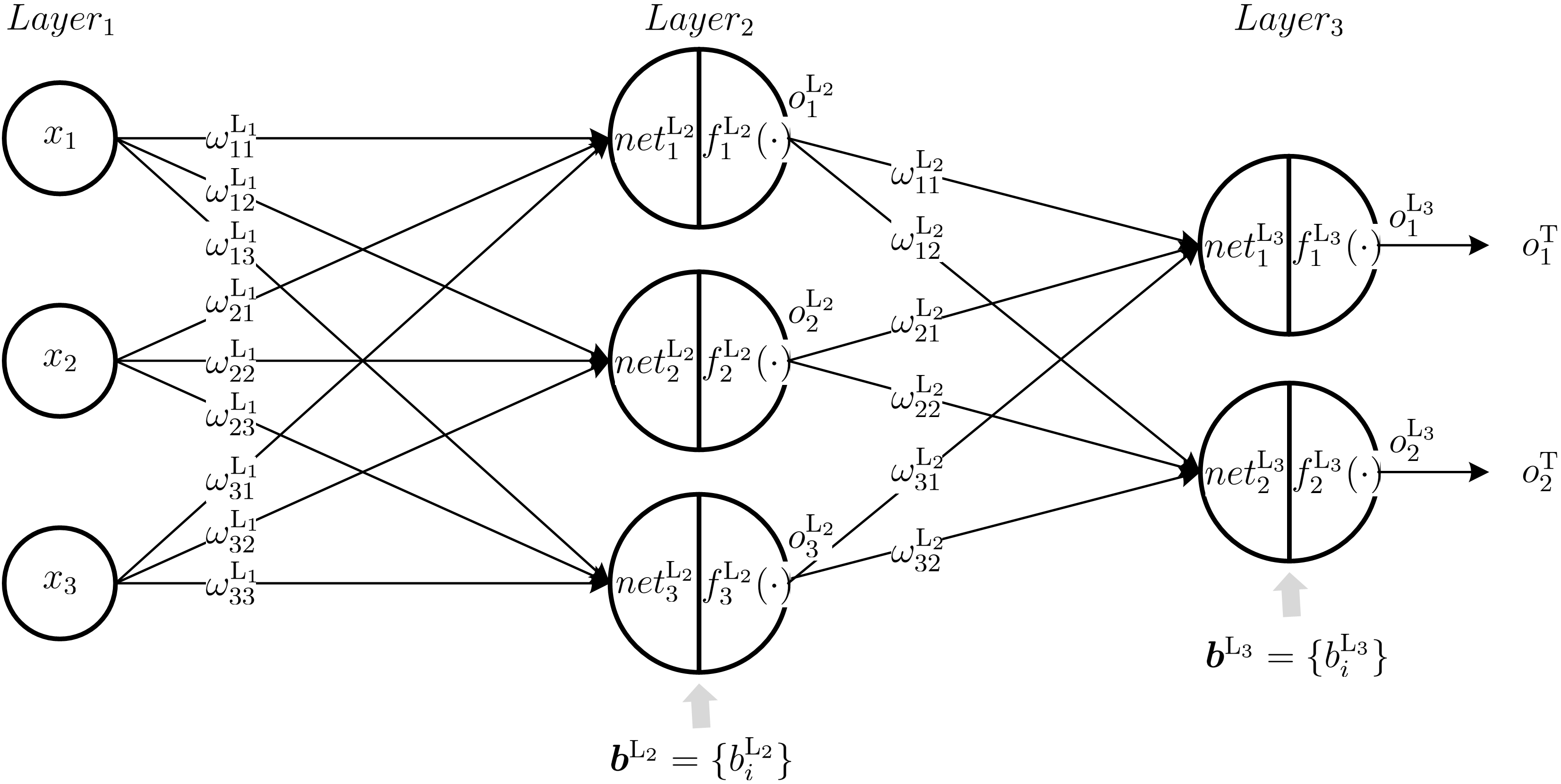
如图所示三层神经网络:输入层 $Layer_1$、隐含层 $Layer_2$、输出层 $Layer_3$.输入层包括三个神经元,即输入为 $\boldsymbol{x}=\lbrace x_1,x_2,x_3 \rbrace$,输出为 $\boldsymbol{y}=\lbrace o_1,o_2 \rbrace$.样本数据集为 \(\mathcal{D}=\lbrace (\boldsymbol{x}_i,\boldsymbol{y}_i)\rbrace_{i=1}^{m}\),\(\boldsymbol{x}_i \in \mathbb{R}^3\),\(\boldsymbol{y}_i \in \mathbb{R}^2\),目标输出为 \(o^{\text{T}}_1\) 和 \(o^{\text{T}}_2\).\(\omega^{\text{L}_k}_{ij}\) 为第 \(k-1\) 层的第 \(i\) 个神经元到第 \(k\) 层的第 \(j\) 个神经元之间的权重.\(\boldsymbol{b}^{\text{L}_k}=\{b^{\text{L}_k}_{i}\}\) 为第 \(k\) 层神经元偏移量集合,\(b^{\text{L}_k}_{i}\) 为第 \(k\) 层第 \(i\) 个神经元的偏移量.\(net^{\text{L}_k}_{i}\) 表示第 \(k\) 层网络的第 \(i\) 个神经元的输入,\(o^{\text{L}_k}_{i}\) 表示第 \(k\) 层网络的第 \(i\) 个神经元的输出,\(f^{\text{L}_k}_{i}(\cdot)\) 表示第 $k$ 层网络的第 $i$ 个神经元的激活函数.
假设采用常见的激活函数 sigmoid 函数: \begin{equation} f(x) = \frac{1}{1+e^{-x}} \end{equation} 其导数为: \begin{equation} f’(x) = f(x)(1-f(x)) \end{equation}
对于 $Layer_2$ 层第 $j$ 个神经元的输入:
\[\begin{equation} net^{\text{L}_2}_{j} = \sum_{i=1}^{3}{\omega^{\text{L}_1}_{ij} \times x_i} + b^{\text{L}_2}_{j} \end{equation}\]对于 $Layer_3$ 层的第 $j$ 个神经元的输入:
\[\begin{equation} net^{\text{L}_3}_{j} = \sum_{i=1}^{3}{\omega^{\text{L}_2}_{ij} \times o^{\text{L}_2}_i} + b^{\text{L}_3}_{j} \end{equation}\]第 \(\text{L}_i\) 层的第 \(j\) 个神经元的输出:
\[\begin{equation}\label{eqn:output of BP neural networks} o^{\text{L}_i}_{j} = f^{\text{L}_i}_{j}{(net^{\text{L}_i}_j)} = \frac{1}{1+e^{-net^{\text{L}_i}_j}} \end{equation}\]输出的总误差为:
\[\begin{equation} E_{\text{Total}} = \frac{1}{2}\sum_{j=1}^{2}{(o^{\text{T}}_j - o^{\text{L}_3}_{j})^2} = \frac{1}{2}((o^{\text{T}}_1 - o^{\text{L}_3}_{1})^2 + (o^{\text{T}}_2 - o^{\text{L}_3}_{2})^2) \end{equation}\]总误差为是关于 \(o^{\text{L}_3}_{1}\) 和 \(o^{\text{L}_3}_{2}\) 的函数.
BP 算法基于梯度下降(gradient descent)策略,以目标的负梯度方向对参数进行调整.它是一个迭代学习算法,在迭代的每一轮中采用广义的感知机学习 规则对参数进行更新估计,任一参数 $v$ 的更新估计式为
\[\begin{equation} v \leftarrow v + \Delta v \end{equation}\]A.$Layer_2$ 与 $Layer_3$ 间参数调整
调整 $Layer_2$ 与 $Layer_3$ 间的权重 \(\omega^{\text{L}_2}_{ij}\).总误差对 \(\omega^{\text{L}_2}_{ij}\) 的偏导数为:
\[\begin{align} \frac{\partial E_{\text{Total}}}{\partial \omega^{\text{L}_2}_{ij}} &= \frac{\partial E_{\text{Total}}}{\partial o^{\text{L}_3}_{j}} \cdot \frac{\partial o^{\text{L}_3}_{j}}{\partial net^{\text{L}_3}_{j}} \cdot \frac{\partial net^{\text{L}_3}_{j}}{\partial \omega^{\text{L}_2}_{ij}} \\ &= -(o^{\text{T}}_{j} - o^{\text{L}_3}_{j}) \cdot f^{\text{L}_3}_{j}{(net^{\text{L}_3}_j)}(1 - f^{\text{L}_3}_{j}{(net^{\text{L}_3}_j)}) \cdot o^{\text{L}_2}_{i} \nonumber\\ &= -(o^{\text{T}}_{j} - o^{\text{L}_3}_{j}) \cdot o^{\text{L}_3}_{j}(1 - o^{\text{L}_3}_{j}) \cdot o^{\text{L}_2}_{i} \nonumber \end{align}\]令 \(\delta^{\text{L}_2}_{ij}\) 表示 $Layer_2$ 层第 $i$ 个神经元与 $Layer_3$ 层第 $j$ 个神经元间权重的梯度项,则
\[\begin{equation} \delta^{\text{L}_2}_{ij} = \frac{\partial E_{\text{Total}}}{\partial o^{\text{L}_3}_{j}} \cdot \frac{\partial o^{\text{L}_3}_{j}}{\partial net^{\text{L}_3}_{j}} = -(o^{\text{T}}_{j} - o^{\text{L}_3}_{j}) \cdot o^{\text{L}_3}_{j}(1 - o^{\text{L}_3}_{j}) \end{equation}\]可以看出, $Layer_2$ 层第 $i$ 个神经元与 $Layer_3$ 层第 $j$ 个神经元间权重的梯度项是与 $i$ 无关的,故连接至 $Layer_3$ 层第 $j$ 个神经元相对应的权重的梯度项均为 \(\delta^{\text{L}_2}_{ij}\),用 \(\delta^{\text{L}_2}_{\cdot j}\) 表示,
\[\begin{equation}\label{eqn:Gradient computation between L2 and L3} \delta^{\text{L}_2}_{\cdot j} = \delta^{\text{L}_2}_{ij} = -(o^{\text{T}}_{j} - o^{\text{L}_3}_{j}) \cdot o^{\text{L}_3}_{j}(1 - o^{\text{L}_3}_{j}) \end{equation}\]则整体误差 \(E_{\text{Total}}\) 对 \(\omega^{\text{L}_2}_{ij}\) 的偏导数公式写作:
\[\begin{equation} \frac{\partial E_{\text{Total}}}{\partial \omega^{\text{L}_2}_{ij}} = \delta^{\text{L}_2}_{\cdot j} \cdot o^{\text{L}_2}_{i} \end{equation}\]则权重 \(\omega^{\text{L}_2}_{ij}\) 的学习公式为:
\[\begin{align}\label{eqn:Self-updating formular for weights between L2 and L3} \widehat{\omega}^{\text{L}_2}_{ij} &= \omega^{\text{L}_2}_{ij} - \eta \cdot \frac{\partial E_{\text{Total}}}{\partial \omega^{\text{L}_2}_{ij}} \\ &= \omega^{\text{L}_2}_{ij} - \eta \cdot \delta^{\text{L}_2}_{\cdot j} \cdot o^{\text{L}_2}_{i} \nonumber \end{align}\]其中,$\eta$ 为学习速率.
调整 $Layer_3$ 的偏移量参数.$Layer_3$ 的第 $j$ 个神经元的偏移量 \(b^{\text{L}_3}_{j}\) 的梯度为:
\[\begin{align} \frac{\partial E_{\text{Total}}}{\partial b^{\text{L}_3}_{j}} &= \frac{\partial E_{\text{Total}}}{\partial o^{\text{L}_3}_{j}} \cdot \frac{\partial o^{\text{L}_3}_{j}}{\partial net^{\text{L}_3}_{j}} \cdot \frac{\partial net^{\text{L}_3}_{j}}{\partial b^{\text{L}_3}_{j}} \\ &= -(o^{\text{T}}_{j} - o^{\text{L}_3}_{j}) \cdot f^{\text{L}_3}_{j}{(net^{\text{L}_3}_j)}(1 - f^{\text{L}_3}_{j}{(net^{\text{L}_3}_j)}) \cdot 1 \nonumber\\ &= -(o^{\text{T}}_{j} - o^{\text{L}_3}_{j}) \cdot o^{\text{L}_3}_{j}(1 - o^{\text{L}_3}_{j}) \nonumber\\ &= \delta^{\text{L}_2}_{\cdot j} \nonumber \end{align}\]偏移 \(b^{\text{L}_3}_{j}\) 的学习公式为:
\[\begin{equation}\label{eqn:Self-updating formular for bias in L3} \hat{b}^{\text{L}_3}_{j} = b^{\text{L}_3}_{j} - \eta \cdot \frac{\partial E_{\text{Total}}}{\partial b^{\text{L}_3}_{j}} = b^{\text{L}_3}_{j} - \eta \cdot \delta^{\text{L}_2}_{\cdot j} \end{equation}\]例如,依据公式(\ref{eqn:Self-updating formular for weights between L2 and L3}),对于权重 \(\omega^{\text{L}_2}_{11}\) 的更新学习公式为:
\[\begin{align*} \widehat{\omega}^{\text{L}_2}_{11} &= \omega^{\text{L}_2}_{11} - \eta \cdot \frac{\partial E_{\text{Total}}}{\partial \omega^{\text{L}_2}_{11}} \\ &= \omega^{\text{L}_2}_{11} - \eta \cdot \delta^{\text{L}_2}_{11} \cdot o^{\text{L}_2}_{1} \\ &= \omega^{\text{L}_2}_{11} - \eta \cdot \big(-(o^{\text{T}}_{1} - o^{\text{L}_3}_{1}) \cdot o^{\text{L}_3}_{1}(1 - o^{\text{L}_3}_{1})\big) \cdot o^{\text{L}_2}_{1} \\ &= \omega^{\text{L}_2}_{11} + \eta \cdot (o^{\text{T}}_{1} - o^{\text{L}_3}_{1}) \cdot o^{\text{L}_3}_{1}(1 - o^{\text{L}_3}_{1}) \cdot o^{\text{L}_2}_{1} \end{align*}\]例如,依据公式(\ref{eqn:Self-updating formular for bias in L3}),对于偏移 \(b^{\text{L}_3}_{1}\) 的更新学习公式为:
\[\begin{align*} \hat{b}^{\text{L}_3}_{1} &= b^{\text{L}_3}_{1} - \eta \cdot \frac{\partial E_{\text{Total}}}{\partial b^{\text{L}_3}_{1}} \\ &= b^{\text{L}_3}_{1} + \eta \cdot (o^{\text{T}}_{1} - o^{\text{L}_3}_{1}) \cdot o^{\text{L}_3}_{1}(1 - o^{\text{L}_3}_{1}) \end{align*}\]B.$Layer_1$ 与 $Layer_2$ 间参数调整
调整 $Layer_1$ 与 $Layer_2$ 间的权重 \(\omega^{\text{L}_1}_{ij}\).总体误差对 \(\omega^{\text{L}_1}_{ij}\) 的偏导数为:
\[\begin{align} \frac{\partial E_{\text{Total}}}{\partial \omega^{\text{L}_1}_{ij}} &= (\sum_{k=1}^{2}{\frac{\partial E_{\text{Total}}}{\partial o^{\text{L}_3}_{k}} \frac{\partial o^{\text{L}_3}_{k}}{\partial net^{\text{L}_3}_k} \frac{\partial net^{\text{L}_3}_k}{\partial o^{\text{L}_2}_{j}}}) \cdot \frac{\partial o^{\text{L}_2}_{j}}{\partial net^{\text{L}_2}_j} \cdot \frac{\partial net^{\text{L}_2}_j}{\partial \omega^{\text{L}_1}_{ij}} \\ &= (\sum_{k=1}^{2}{\delta^{\text{Layer}_2}_{\cdot k} \omega^{\text{L}_2}_{3k}}) \cdot f^{\text{L}_2}_{j}{(net^{\text{L}_2}_j)}(1 - f^{\text{L}_2}_{j}{(net^{\text{L}_2}_j)}) \cdot x_i \nonumber\\ &= (\sum_{k=1}^{2}{\delta^{\text{Layer}_2}_{\cdot k} \omega^{\text{L}_2}_{3k}}) \cdot o^{\text{L}_2}_{j}(1 - o^{\text{L}_2}_{j}) \cdot x_i \nonumber \end{align}\]令 \(\delta^{\text{L}_1}_{ij}\) 表示 $Layer_1$ 层第 $i$ 个神经元与 $Layer_2$ 层第 $j$ 个神经元间权重的梯度项,则
\[\begin{align} \delta^{\text{L}_1}_{ij} &= (\sum_{k=1}^{2}{\frac{\partial E_{\text{Total}}}{\partial o^{\text{L}_3}_{k}} \frac{\partial o^{\text{L}_3}_{k}}{\partial net^{\text{L}_3}_k} \frac{\partial net^{\text{L}_3}_k}{\partial o^{\text{L}_2}_{j}}}) \cdot \frac{\partial o^{\text{L}_2}_{j}}{\partial net^{\text{L}_2}_j} \\ &= (\sum_{k=1}^{2}{\delta^{\text{Layer}_2}_{\cdot k} \omega^{\text{L}_2}_{3k}}) \cdot o^{\text{L}_2}_{j}(1 - o^{\text{L}_2}_{j}) \nonumber \end{align}\]可以看出, $Layer_1$ 层第 $i$ 个神经元与 $Layer_2$ 层第 $j$ 个神经元间权重的梯度项是与 $i$ 无关的,故连接至 $Layer_2$ 层第 $j$ 个神经元相对应的权重的梯度向均为 \(\delta^{\text{L}_1}_{ij}\),用 \(\delta^{\text{L}_1}_{\cdot j}\) 表示,
\[\begin{equation}\label{eqn:Gradient computation between L1 and L2} \delta^{\text{L}_1}_{\cdot j} = \delta^{\text{L}_1}_{ij} = (\sum_{k=1}^{2}{\delta^{\text{Layer}_2}_{\cdot k} \omega^{\text{L}_2}_{3k}}) \cdot o^{\text{L}_2}_{j}(1 - o^{\text{L}_2}_{j}) \end{equation}\]则整体误差 \(E_{\text{Total}}\) 对 \(\omega^{\text{L}_1}_{ij}\) 的偏导数公式写作:
\[\begin{equation} \frac{\partial E_{\text{Total}}}{\partial \omega^{\text{L}_1}_{ij}} = \delta^{\text{L}_1}_{\cdot j} \cdot x_i \end{equation}\]则权重 \(\omega^{\text{L}_1}_{ij}\) 的学习公式为:
\[\begin{equation}\label{eqn:Self-updating formular for weights between L1 and L2} \widehat{\omega}^{\text{L}_1}_{ij} = \omega^{\text{L}_1}_{ij} - \eta \cdot \frac{\partial E_{\text{Total}}}{\partial \omega^{\text{L}_1}_{ij}} = \omega^{\text{L}_1}_{ij} - \eta \cdot \delta^{\text{L}_1}_{\cdot j} \cdot x_i \end{equation}\]整体误差 \(E_{\text{Total}}\) 对 \(b^{\text{L}_2}_{j}\) 的偏导数公式写作:
\[\begin{align} \frac{\partial E_{\text{Total}}}{\partial b^{\text{L}_2}_{j}} &= (\sum_{k=1}^{2}{\frac{\partial E_{\text{Total}}}{\partial o^{\text{L}_3}_{k}} \frac{\partial o^{\text{L}_3}_{k}}{\partial net^{\text{L}_3}_k} \frac{\partial net^{\text{L}_3}_k}{\partial o^{\text{L}_2}_{j}}}) \cdot \frac{\partial o^{\text{L}_2}_{j}}{\partial net^{\text{L}_2}_j} \cdot \frac{\partial net^{\text{L}_2}_j}{\partial b^{\text{L}_2}_{j}} \\ &= (\sum_{k=1}^{2}{\delta^{\text{Layer}_2}_{\cdot k} \omega^{\text{L}_2}_{3k}}) \cdot f^{\text{L}_2}_{j}{(net^{\text{L}_2}_j)}(1 - f^{\text{L}_2}_{j}{(net^{\text{L}_2}_j)}) \cdot 1 \nonumber\\ &= (\sum_{k=1}^{2}{\delta^{\text{Layer}_2}_{\cdot k} \omega^{\text{L}_2}_{3k}}) \cdot o^{\text{L}_2}_{j}(1 - o^{\text{L}_2}_{j}) \nonumber\\ &= \delta^{\text{L}_1}_{\cdot j} \nonumber \end{align}\]偏移 \(b^{\text{L}_2}_{j}\) 的学习公式为:
\[\begin{equation}\label{eqn:Self-updating formular for bias in L2} \hat{b}^{\text{L}_2}_{j} = b^{\text{L}_2}_{j} - \eta \cdot \frac{\partial E_{\text{Total}}}{\partial b^{\text{L}_2}_{j}} = b^{\text{L}_2}_{j} - \eta \cdot \delta^{\text{L}_1}_{\cdot j} \end{equation}\]例如,依据公式(\ref{eqn:Self-updating formular for weights between L1 and L2})对于权重 \(\omega^{\text{L}_1}_{23}\) 的更新学习公式为:
\[\begin{align}\label{eq2:description} \widehat{\omega}^{\text{L}_1}_{23} &= \omega^{\text{L}_2}_{23} - \eta \cdot \frac{\partial E_{\text{Total}}}{\partial \omega^{\text{L}_1}_{23}} \\ &= \omega^{\text{L}_2}_{23} - \eta \cdot \big((\sum_{j=1}^{2}{\frac{\partial E_{\text{Total}}}{\partial o^{\text{L}_3}_{j}} \frac{\partial o^{\text{L}_3}_{j}}{\partial net^{\text{L}_3}_j} \frac{\partial net^{\text{L}_3}_j}{\partial o^{\text{L}_2}_{3}}}) \cdot \frac{\partial o^{\text{L}_2}_{3}}{\partial net^{\text{L}_2}_3} \cdot \frac{\partial net^{\text{L}_2}_3}{\partial \omega^{\text{L}_1}_{23}}\big) \nonumber\\ &= \omega^{\text{L}_2}_{23} - \eta \cdot (\sum_{j=1}^{2}{\delta^{\text{Layer}_2}_{\cdot j} \omega^{\text{L}_2}_{3j}}) \cdot f^{\text{L}_2}_{3}{(net^{\text{L}_2}_3)}(1 - f^{\text{L}_2}_{3}{(net^{\text{L}_2}_3)}) \cdot x_2 \nonumber\\ &= \omega^{\text{L}_2}_{23} - \eta \cdot (\sum_{j=1}^{2}{\delta^{\text{Layer}_2}_{\cdot j} \omega^{\text{L}_2}_{3j}}) \cdot o^{\text{L}_2}_{3}(1 - o^{\text{L}_2}_{3}) \cdot x_2 \nonumber \end{align}\]例如,依据公式(\ref{eqn:Self-updating formular for bias in L2}),对于偏移 \(b^{\text{L}_2}_{3}\) 的更新学习公式为:
\[\begin{align}\label{eq1:description} \hat{b}^{\text{L}_2}_{3} &= b^{\text{L}_3}_{1} - \eta \cdot \frac{\partial E_{\text{Total}}}{\partial b^{\text{L}_2}_{3}} \\ &= b^{\text{L}_2}_{3} - \eta \cdot \big((\sum_{j=1}^{2}{\frac{\partial E_{\text{Total}}}{\partial o^{\text{L}_3}_{j}} \frac{\partial o^{\text{L}_3}_{j}}{\partial net^{\text{L}_3}_j} \frac{\partial net^{\text{L}_3}_j}{\partial o^{\text{L}_2}_{3}}}) \cdot \frac{\partial o^{\text{L}_2}_{3}}{\partial net^{\text{L}_2}_3} \cdot \frac{\partial net^{\text{L}_2}_3}{\partial b^{\text{L}_2}_{3}}\big) \nonumber\\ &= b^{\text{L}_2}_{3} - \eta \cdot (\sum_{j=1}^{2}{\delta^{\text{Layer}_2}_{\cdot j} \omega^{\text{L}_2}_{3j}}) \cdot f^{\text{L}_2}_{3}{(net^{\text{L}_2}_3)}(1 - f^{\text{L}_2}_{3}{(net^{\text{L}_2}_3)}) \cdot 1 \nonumber\\ &= b^{\text{L}_2}_{3} - \eta \cdot (\sum_{j=1}^{2}{\delta^{\text{Layer}_2}_{\cdot j} \omega^{\text{L}_2}_{3j}}) \cdot o^{\text{L}_2}_{3}(1 - o^{\text{L}_2}_{3}) \nonumber \end{align}\]需要指出的是学习率 $\eta \in (0,1)$ 控制着算法每一轮迭代中的更新步长,若太多则容易震荡;太小则收敛速录又会过慢.并且公式(\ref{eqn:Self-updating formular for weights between L2 and L3})、(\ref{eqn:Self-updating formular for bias in L3})、(\ref{eqn:Self-updating formular for weights between L1 and L2})和(\ref{eqn:Self-updating formular for bias in L2})中的学习率也未必相等.
C.误差反向传播算法
结合上述公式,根据样本参数计算总体误差;根据总体误差,更新神经网络参数;这样,实现信号的正向传递,误差的反向传播,参数的自适应.如此,不停的进行迭代直至满足停止条件.
具体而言,BP 算法执行以下操作:先将输入示例提供给输入层神经元,然后逐层将信号前传,直到产生输出层的结果;然后计算输出层的误差,再将误差逆向传播至隐层神经元,最后根据隐层神经元的误差来别连接权和偏移进行调整.该法代过程循环进行,直到达到某些停止条件为止,例如训练误差己达到一个很小的值.具体操作流程如下所示.
输入:训练集 \(\mathcal{D}=\lbrace (\boldsymbol{x}_i,\boldsymbol{y}_i)\rbrace_{i=1}^{m}\)
学习率 $\eta$
过程:
- 在 $(0,1)$ 范围内随机初始化网络中所有连接权重和偏移量
- repeat
- for all \((\boldsymbol{x}_k,\boldsymbol{y}_k) \in \mathcal{D}\) do
- 根据当前参数和式(\ref{eqn:output of BP neural networks})计算当前样本的输出\(o^{\text{L}_3}_{j}\)
- 根据式(\ref{eqn:Gradient computation between L2 and L3})计算输出层神经元的梯度项 \(\delta^{\text{L}_2}_{\cdot j}\)
- 根据式(\ref{eqn:Gradient computation between L1 and L2})计算隐含层各神经元的梯度项 \(\delta^{\text{L}_1}_{\cdot j}\)
- 根据式(\ref{eqn:Self-updating formular for weights between L2 and L3})和(\ref{eqn:Self-updating formular for bias in L3})更新连接权重 \(\omega^{\text{L}_3}_{ij}\) 和偏移 \(b^{\text{L}_3}_{j}\)
- 根据式(\ref{eqn:Self-updating formular for weights between L1 and L2})和(\ref{eqn:Self-updating formular for bias in L2})更新连接权重\(\omega^{\text{L}_2}_{ij}\) 和偏移 \(b^{\text{L}_2}_{j}\)
- end for
- until 达到停止条件
- 输出:连接权重与偏移量确定的多层前馈神经网络
扩展
上面介绍为“标准 BP 算法”,每次仅针对一个训练样例更新权重和偏移,也就是说,算法的更新规则是基于单个的样本的误差推导而得.
如果类似地推导出基于累积误差最小化的更新规则,就得到了累积误差逆传播(accumulated error backpropagation)算法.累积 BP 算法与标准 BP 算法都很常用.一般来说,标准 BP 算法每次更新只针对单个样例,参数更新得非常频繁,而且对不同样例进行更新的效果可能出现“抵消”现象.因此,为了达到同样的累积误差极小点,标准 BP 算法往往需进行更多次数的法代.累积 BP 算法直接针对累积误差最小化,它在读取整个训练集 \(\mathcal{D}\) 一遍后才对参数进行更新,其参数更新的频率低得多.但在很多任务中,累积误差下降到一定程度之后,进一步下降会非常缓慢,这时标准 BP 往往会更快获得较好的解,尤其是在训练集 \(\mathcal{D}\) 非常大时更明显.
