目录
NSGA-II 简介
Nondominated Sorting Genetic Algorithm II (NSGA-II),又名 a nondominated sorting-based multiobjective EA (MOEA),是由 NSGA 改进而来的,用于解决复杂的、多目标优化问题。该算法是 K-Deb 在 2002 年论文《A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II》中提出。
针对 NSGA 中存在的问题:1)复杂度 \(O(MN^3)\),\(M\) 为优化目标个数,\(N\) 为种群规模;2)非精英主义;3)需要指定共享参数,该参数将对种群的多样性产生很大的影响。与此相比, NSGA-II 有几个特点:1)复杂度相对较低,为 \(O(MN^2)\) ;2)维护了精英个体,即在迭代过程中保留了最为精英的部分;3)不需要用户指定类似共享参数之列的参数,减少用户主观指定的参数,NSGA-II中从新定义了拥挤距离代替共享参数。
NSGA-II 主流程
NSGA-II 主循环流程与一般的 GA 类似,在构建后代种群是方法尤其独特性,其具体步骤为:
- 构建新一代种群:父代 + 子代
- 对新一代种群进行非支配排序和拥挤距离评估
- 精选新一代种群个体:对于不同支配等级的个体,优选支配等级小的个体;对于拥有相同支配等级的,选择拥挤距离大的个体;
- 对该种群进行交叉、变异操作,产生子代种群;
其主要流程如下:
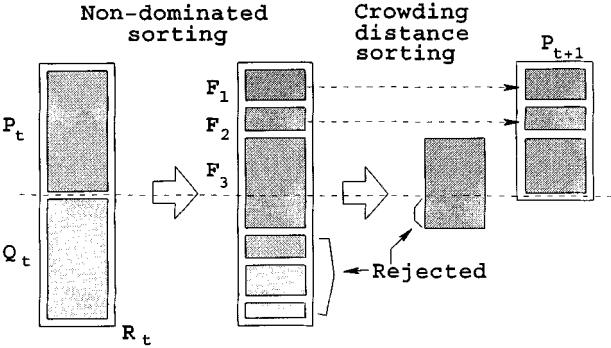
伪代码如下所示:

快速非支配排序
提及多目标优化,一般需要了解 Pareto Optimal,快速非支配排序就是依据此进行排序。对于 Pareto Optimal 的概念这里不做介绍,感兴趣的读者可以自行查阅。
快速非支配排序中的 2 个概念:
- 被支配个体集合 \(S_p\) : 解空间中,可以支配个体 \(p\) 的所有个体构成的集合;
- 支配个体数 \(n_p\) : 解空间中,被个体 \(p\) 支配的所有个体的数量;
其主要步骤如下:
- 计算每个个体的 \(n_p\) 和 \(S_p\)
- \(n_p=0\) 的个体归属于 \(\mathcal{F}_1\);然后令这些个体的 \(S_p\) 所有个体的 \(n_p-1\);
- \(n_p=0\) 的个体归属于 \(\mathcal{F}_2\);以此类推,直到所有个体处理完毕;
其伪代码如下:

上述算法的时间复杂度为\(O(M(2N)^2)\)。
多样性保留
在 NSGA 中通过共享参数保持解能相对均匀分布,也就是尽量要保持解的多样性。对于 NSGA-II 则是采用拥挤距离来维持种群多样性。
拥挤距离定义如下:拥挤距离等于解在各个目标函数的方向上的前后两个解的距离和。在二维时,就等于图像矩形轴周长的一半。
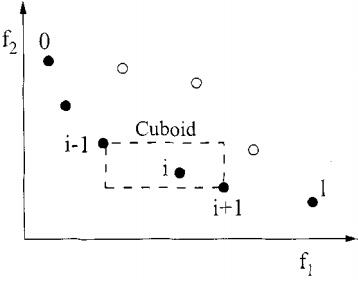
其计算的伪代码如下:
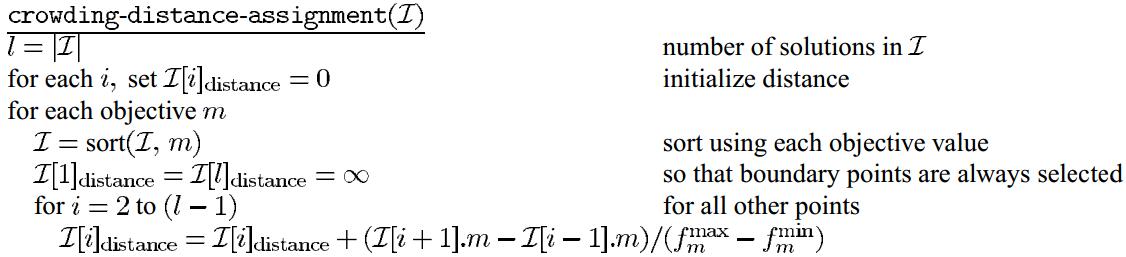
上述算法的时间复杂度为\(O(M(2N)log(2N))\)。
注意:如果某个方向上的距离很大,就会很大程度上影响总的距离的大小。为了使每个方向上的目标函数对拥挤距离有等效的影响力(无量纲化),需要每个目标函数上的距离要规则化normalized。
在进行个体选择时,需要比较个体优劣,对于处于不同支配等级的个体,支配等级越低,则越优;对于处于同一支配等级的个体,则比较拥挤距离:距离越大,表明周围解的密度越小,则分布越均匀,则越优。其比较规则如下:

NSGA-II 的代码已在 K-Deb 实验室网站公布:http://www.iitk.ac.in/kangal/codes.shtml,可以下载下来学习。
